O ano de 2020 nos reservou alguns imprevistos, mas isso não significa que precisamos interromper nossos estudos. Por isso dou boas vindas aos alunos do Ensino Médio do Colégio Vila de Cava a esse espaço que usaremos pelas próximas aulas.
Dito isto, gostaria de destacar alguns pontos:
Aqui é uma extensão da sala de aula, então todas as regras de comportamento que valem dentro da escola, valem aqui também.
Os conteúdos aqui apresentados podem ser cobrados nas próximas avaliações presenciais, por isso é muito importante que o aluno faça as anotações necessárias sobre a aula para ter o material organizado e preparado para estudar para as provas.
Guarde bem seus registros, pois darei visto nos cadernos quando retornarmos.
É necessário que todos entendam que para ter sucesso no estudo a distância é preciso alguns cuidados:
1- Utilize o tempo que você estaria normalmente na escola para se dedicar aos estudos.
2- Faça as atividades sentado em uma mesa, mesmo que improvisada. Não faça deitado, para evitar sonolência.
3- Não responda a mensagens de amigos ou pare para ver a rede social de ninguém enquanto estiver estudando.
4- Evite ouvir música nesse período.
5- Lembre-se que as atividades serão postadas nos dias e horários que você teria se fosse a escola.
6- Leia com atenção as atividades, faça as anotações importantes no caderno, realize o que foi pedido.
7- Se perceber que passou uma hora e meia estudando direto, pare um pouco. Levante-se, estique as pernas, beba água, coma algo e depois retorne as atividades.
8- Esperamos que você gaste umas 6 horas por dia estudando. Ou mais, se puder.
9- Evite buscar respostas prontas, tente fazer sozinho, se houver dúvidas entre em contato com o professor, só depois tente trocar ideias com os colegas.
10- Não desista!
Então, vamos começar?
Vamos corrigir o dever que passei no último dia de aula presencial que tivemos?
Considere um quadrado Q e um círculo C de área igual a 16π cm². Sabendo que o perímetro do quadrado e o comprimento da circunferência do círculo tem a mesma medida, calcule a área de Q.
Resolução:
A fórmula da área de um círculo é A = πr², pelo enunciado temos que A = 16π, logo:
16π = πr²
r² = 16π
π
r² = 16
r = 4 cm
Ainda pelo enunciado temos que o perímetro de um quadrado tem a mesma medida que o comprimento da circunferência, logo:
Perímetro de um quadrado de lado l = circunferência
4.l = 2πr
4.l = 2π.4 (pois achamos o raio = 4)
4.l = 8π
l = 2π
Como o lado do quadrado é 2π, sua área é dada por A = l², logo:
A = (2π)²
A = 4π² cm²
Página 325. N° 53 e 55
53 - Primeiro, ao dividir 760 por 360, temos como resto 40°, logo tg 760° = tg 40°
Agora vamos comparar as tangente de 40° e de 70°. Repare a imagem abaixo, quanto maior o ângulo x no primeiro quadrante, maior é o valor na reta de tangência.
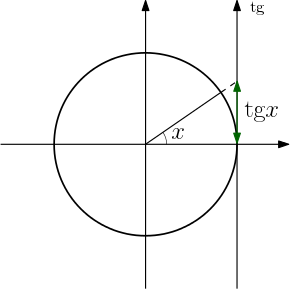
Se ainda tem dúvidas, acesse o Geogebra aqui e mova o ângulo x (o ponto azul), notando como o ponto de tangência (o ponto cinza) se comporta, no primeiro quadrante.
Portanto Tg 70° é maior que Tg 40°.
55 - a) tg π + tg 3π + tg 5π , onde π = 45º
4 4 4 4
É necessário que todos entendam que para ter sucesso no estudo a distância é preciso alguns cuidados:
1- Utilize o tempo que você estaria normalmente na escola para se dedicar aos estudos.
2- Faça as atividades sentado em uma mesa, mesmo que improvisada. Não faça deitado, para evitar sonolência.
3- Não responda a mensagens de amigos ou pare para ver a rede social de ninguém enquanto estiver estudando.
4- Evite ouvir música nesse período.
5- Lembre-se que as atividades serão postadas nos dias e horários que você teria se fosse a escola.
6- Leia com atenção as atividades, faça as anotações importantes no caderno, realize o que foi pedido.
7- Se perceber que passou uma hora e meia estudando direto, pare um pouco. Levante-se, estique as pernas, beba água, coma algo e depois retorne as atividades.
8- Esperamos que você gaste umas 6 horas por dia estudando. Ou mais, se puder.
9- Evite buscar respostas prontas, tente fazer sozinho, se houver dúvidas entre em contato com o professor, só depois tente trocar ideias com os colegas.
10- Não desista!
Então, vamos começar?
Vamos corrigir o dever que passei no último dia de aula presencial que tivemos?
1° ano
Página 33, n°30:Considere um quadrado Q e um círculo C de área igual a 16π cm². Sabendo que o perímetro do quadrado e o comprimento da circunferência do círculo tem a mesma medida, calcule a área de Q.
Resolução:
A fórmula da área de um círculo é A = πr², pelo enunciado temos que A = 16π, logo:
16π = πr²
r² = 16π
π
r² = 16
r = 4 cm
Ainda pelo enunciado temos que o perímetro de um quadrado tem a mesma medida que o comprimento da circunferência, logo:
Perímetro de um quadrado de lado l = circunferência
4.l = 2πr
4.l = 2π.4 (pois achamos o raio = 4)
4.l = 8π
l = 2π
Como o lado do quadrado é 2π, sua área é dada por A = l², logo:
A = (2π)²
A = 4π² cm²
2° ano
Página 325. N° 53 e 55
53 - Primeiro, ao dividir 760 por 360, temos como resto 40°, logo tg 760° = tg 40°
Agora vamos comparar as tangente de 40° e de 70°. Repare a imagem abaixo, quanto maior o ângulo x no primeiro quadrante, maior é o valor na reta de tangência.

Se ainda tem dúvidas, acesse o Geogebra aqui e mova o ângulo x (o ponto azul), notando como o ponto de tangência (o ponto cinza) se comporta, no primeiro quadrante.
Portanto Tg 70° é maior que Tg 40°.
55 - a) tg π + tg 3π + tg 5π , onde π = 45º
4 4 4 4
logo a expressão fica: tg 45° + tg 135° + tg 225°
Como 135 = 180 - 45, tg 135° = - tg 45°
Como 225 = 180 + 45, tg 225° = tg 45°
E tg 45° = 1, temos que:
tg 45° + tg 135° + tg 225°
1 - 1 + 1 = 1
b) tg -60° + tg -120° + tg -240°
Cada ângulo negativo possui algum ângulo positivo congruente. Para achá-lo, basta adicioná-lo a 360°.
Assim, -60° = -60° + 360° = 300°
-120° = -120° + 360° = 240°
-240° = -240° + 360° = 120°
Logo, a expressão fica:
tg 300° + tg 240° + tg 120°
Como 300 = 360 - 60, tg 300° = -tg 60°
Como 240 = 180 + 60, tg 240° = tg 60°
Como 120 = 180 - 60, tg 120° = - tg 60°
E tg 60° = , temos que:
, temos que:
tg 300° + tg 240° + tg 120°
- +
+  -
-  = -
= - 
m = 3 e n = -7 y = -3x +2
2
m = -3/2 e n = 1
Como os valores de m são diferentes, as retas são concorrentes
b) 3x +2y - 11 = 0 e 3x + 2y = 6
y = -3x +11 y = -3x +6
2 2
m = -3/2 e n = -11/2 m = -3/2 e n = 3
Como os valores de m são iguais, mas os valores de n são diferentes, as retas paralelas.
c) -4x + 3y = - 12 y = 4x -4
y = 4x - 12 3
3 m = 4/3 e n = -4
m= 4/3 e n = - 4
Como tanto os valores de m quanto os de n são iguais, as retas são coincidentes.
ATENÇÃO:
Se você fez as correções e ainda teve dúvidas, deixe um comentário com a dúvida, seu nome e sua turma.
Se você fez a correção e não teve dúvida, deixe um comentário apenas com seu nome e sua turma.
Todo aluno que deixar registrado o comentário receberá aquele positivo lá na minha listinha que já mostrei a vocês, ok?
Até a próxima ;)
Como 135 = 180 - 45, tg 135° = - tg 45°
Como 225 = 180 + 45, tg 225° = tg 45°
E tg 45° = 1, temos que:
tg 45° + tg 135° + tg 225°
1 - 1 + 1 = 1
b) tg -60° + tg -120° + tg -240°
Cada ângulo negativo possui algum ângulo positivo congruente. Para achá-lo, basta adicioná-lo a 360°.
Assim, -60° = -60° + 360° = 300°
-120° = -120° + 360° = 240°
-240° = -240° + 360° = 120°
Logo, a expressão fica:
tg 300° + tg 240° + tg 120°
Como 300 = 360 - 60, tg 300° = -tg 60°
Como 240 = 180 + 60, tg 240° = tg 60°
Como 120 = 180 - 60, tg 120° = - tg 60°
E tg 60° =
 , temos que:
, temos que:tg 300° + tg 240° + tg 120°
-
 +
+  -
-  = -
= - 
3° ano
a) y = 3x -7 e 3x + 2y - 2 = 0m = 3 e n = -7 y = -3x +2
2
m = -3/2 e n = 1
Como os valores de m são diferentes, as retas são concorrentes
b) 3x +2y - 11 = 0 e 3x + 2y = 6
y = -3x +11 y = -3x +6
2 2
m = -3/2 e n = -11/2 m = -3/2 e n = 3
Como os valores de m são iguais, mas os valores de n são diferentes, as retas paralelas.
c) -4x + 3y = - 12 y = 4x -4
y = 4x - 12 3
3 m = 4/3 e n = -4
m= 4/3 e n = - 4
Como tanto os valores de m quanto os de n são iguais, as retas são coincidentes.
ATENÇÃO:
Se você fez as correções e ainda teve dúvidas, deixe um comentário com a dúvida, seu nome e sua turma.
Se você fez a correção e não teve dúvida, deixe um comentário apenas com seu nome e sua turma.
Todo aluno que deixar registrado o comentário receberá aquele positivo lá na minha listinha que já mostrei a vocês, ok?
Até a próxima ;)


Jorge Eduardo Ricce telles
ResponderExcluir2° ano médio
Maria Vitória
ResponderExcluir1°ano médio
Yasmin Pimentel
ResponderExcluir1°ano médio
Gabriel Ferreira
ResponderExcluirMaria Eduarda Honorato 3°ano médio
ResponderExcluirSara Cintia
ResponderExcluir1°ano
Diogo
ResponderExcluir2°ano
Millena Barros
ResponderExcluir3* ano médio