Vamos corrigir o dever da última aula:
6) x = 12 cm
10) 25 m
12) Fazendo \[\frac{CD}{BC}=\frac{BC}{AC}\], temos CD = 3,2 cm
13) Como os ângulos dos triângulos ABC e AED são congruentes entre si, esses triângulos são semelhantes. Portanto, é válida a relação:
\[\frac{0,8}{2,2} = \frac{3,2}{(3,2 + x)}\]
\[0,8. (3,2 + x) = 2,2 ⋅ 3,2\]
\[0,8x + 2,56 = 7,04\]
\[0,8x = 7,04 – 2,56\]
\[x = \frac{4,48}{0,8} = 5,6\]
Hoje a aula é sobre um assunto que vocês já viram ano passado: Trigonometria.
Vamos recordar?
Lembre-se de anotar no caderno as informações principais, como definições e fórmulas.
A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.
Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.
Tabela Trigonométrica
Na tabela trigonométrica consta o valor de cada razão trigonométrica para os ângulos de 1º a 90º.
Os ângulos de 30º, 45º e 60º são os mais usados nos cálculos e por isso, eles são chamados de ângulos notáveis.

Para compreender melhor a aplicação das fórmulas, confira abaixo dois exemplos:
EXEMPLO 1) Encontre os valores do seno, cosseno e tangente do ângulo do triângulo abaixo.
do triângulo abaixo.
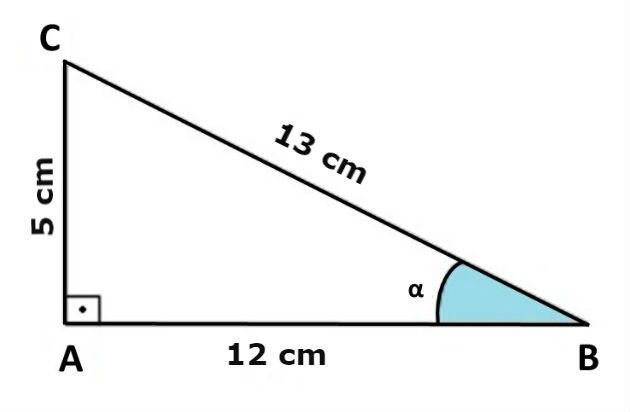
Solução
Para encontrar os valores do seno, cosseno e tangente, devemos substituir a medida de cada lado do triângulo nas respectivas fórmulas.
Observando a imagem, identificamos que o cateto oposto mede 5 cm, o cateto adjacente mede 12 cm e a medida da hipotenusa é igual a 13 cm. Assim, temos:



EXEMPLO 2) Determine o valor de x na figura abaixo.
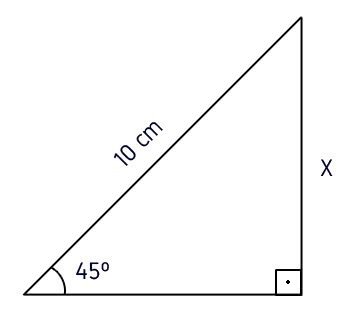
Observe que temos a medida da hipotenusa (10 cm) e queremos descobrir a medida de x, que é o cateto oposto ao ângulo de 45º. Desta forma, aplicaremos a fórmula do seno.
De acordo com a tabela trigonométrica, o valor do seno de 45.º é aproximadamente igual a 0,7071. Assim:

Portanto, o lado x mede 7,071 cm.
EXEMPLO 3) Qual o comprimento da sombra de uma árvore de 5 m de altura quando o sol está a 30° acima do horizonte? (Use Sen 30° = 0,5 ou cos 30° = 0,70 ou Tg 30° = 0,57)
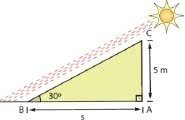
O primeiro passo para resolver é descobrir se usaremos o seno, o cosseno ou o tangente dado no enunciado. (Repare que eu não tenho o valor da hipotenusa, apenas os catetos, pela figura o adjacente do ângulo de 30° que mede s e o oposto mede 5)
Imprima ou copie e resolva esses exercícios no caderno:
https://www.somatematica.com.br/soexercicios/razoesTrig.php
Até a próxima.
\[0,8. (3,2 + x) = 2,2 ⋅ 3,2\]
\[0,8x + 2,56 = 7,04\]
\[0,8x = 7,04 – 2,56\]
\[x = \frac{4,48}{0,8} = 5,6\]
Hoje a aula é sobre um assunto que vocês já viram ano passado: Trigonometria.
Vamos recordar?
Lembre-se de anotar no caderno as informações principais, como definições e fórmulas.
A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.
Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.
Funções Trigonométricas
As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.
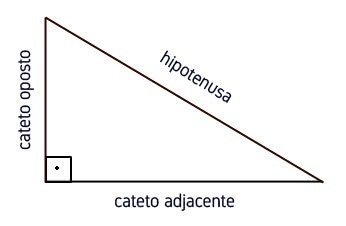
As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
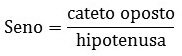
Lê-se cateto oposto sobre a hipotenusa.
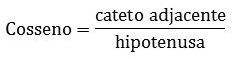
Lê-se cateto adjacente sobre a hipotenusa.
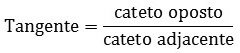
Lê-se cateto oposto sobre cateto adjacente.
As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.

As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
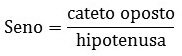
Lê-se cateto oposto sobre a hipotenusa.
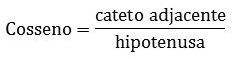
Lê-se cateto adjacente sobre a hipotenusa.
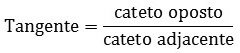
Lê-se cateto oposto sobre cateto adjacente.
Tabela Trigonométrica
Na tabela trigonométrica consta o valor de cada razão trigonométrica para os ângulos de 1º a 90º.
Os ângulos de 30º, 45º e 60º são os mais usados nos cálculos e por isso, eles são chamados de ângulos notáveis.
Para compreender melhor a aplicação das fórmulas, confira abaixo dois exemplos:
EXEMPLO 1) Encontre os valores do seno, cosseno e tangente do ângulo

Solução
Para encontrar os valores do seno, cosseno e tangente, devemos substituir a medida de cada lado do triângulo nas respectivas fórmulas.
Observando a imagem, identificamos que o cateto oposto mede 5 cm, o cateto adjacente mede 12 cm e a medida da hipotenusa é igual a 13 cm. Assim, temos:
EXEMPLO 2) Determine o valor de x na figura abaixo.

Observe que temos a medida da hipotenusa (10 cm) e queremos descobrir a medida de x, que é o cateto oposto ao ângulo de 45º. Desta forma, aplicaremos a fórmula do seno.
De acordo com a tabela trigonométrica, o valor do seno de 45.º é aproximadamente igual a 0,7071. Assim:
Portanto, o lado x mede 7,071 cm.
EXEMPLO 3) Qual o comprimento da sombra de uma árvore de 5 m de altura quando o sol está a 30° acima do horizonte? (Use Sen 30° = 0,5 ou cos 30° = 0,70 ou Tg 30° = 0,57)

O primeiro passo para resolver é descobrir se usaremos o seno, o cosseno ou o tangente dado no enunciado. (Repare que eu não tenho o valor da hipotenusa, apenas os catetos, pela figura o adjacente do ângulo de 30° que mede s e o oposto mede 5)
Como a tangente é a que usa apenas os catetos, é ela que usaremos nessa questão.
Tg B = cateto oposto
cateto adjacente
Usando as informações do problema temos:
0,57 = 5
s
s = 5
Usando as informações do problema temos:
0,57 = 5
s
s = 5
0,57
s = 8,77
Portanto, o tamanho da sombra é de 8,77 metros.
Portanto, o tamanho da sombra é de 8,77 metros.
Imprima ou copie e resolva esses exercícios no caderno:
https://www.somatematica.com.br/soexercicios/razoesTrig.php
Até a próxima.
Se não conseguiu visualizar o formulário de presença obrigatório, acesse-o em https://forms.gle/S6962qKHn5XLuE8R6


0 comentários:
Postar um comentário