Aula I Exercícios de Fixação - 1° ano

Olá, turma.

Hoje vamos resolver alguns exercícios sobre Teorema de Tales e Semelhança de Triângulos. Ambos assuntos já foram explicados em sala, mas se quiser relembrar, assista o curto vídeo abaixo:



Se você quiser ver alguns exemplos de exercícios sobre o assunto, é só assistir o vídeo abaixo:



Agora sim, cadernos e canetas a postos! Atacar>

Abra o livro.
Vamos começar com a página 10, números 6 e 7. É bom aproveitar e verificar se você resolveu e corrigiu a página 9, pois fizemos isso tudo em aula.

Para quem não tem o livro, segue o enunciado:

6 - O ∆abc tem lados AB= 15 cm e BC = 20 cm. Uma reta r paralela a AC, intercepta os lados AB e BC nos pontos P e Q respectivamente de modo que BP = 9 cm. Determine a medida x do segmento BQ.

Vamos fazer juntos.

Comece desenhando um triângulo ABC.

Marque nele as informações dadas: AB= 15 cm e BC = 20 cm

Agora trace uma paralela a base AC. Repare que essa reta corta os lados AB e BC, criando novos segmentos BP e BQ. O problema deu que BP = 9 cm e ele quer BQ, logo BQ = x.

Ficou mais ou menos assim:

Pelo Teorema de Tales AB = BP
                                          BC   BQ

Substitua os valores pelos segmentos e finalize a questão.

7- O ∆abc tem 50 cm de perímetro. A bissetriz do Triângulo relativa ao ângulo interno b intercepta o lado AC dividido-o em dois segmentos de medidas 8 cm e 12 cm, sendo o maior deles com a extremidade de C. Calcule as medidas dos outros dois lados desse triângulo.

Novamente, vamos desenhar o que o enunciado deseja.

Uma bissetriz interna é assim:

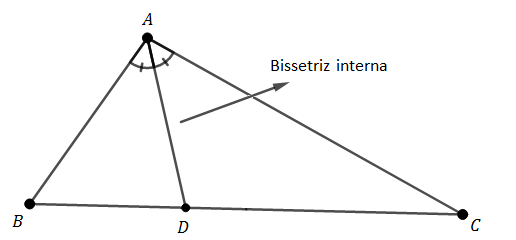
Só que o enunciado quer que a bissetriz parta do ângulo B, e não do A como está na imagem.

Essa bissetriz vai tocar o lado AC cortando-o em duas partes, uma de 8 cm e outra de 12 cm.

Os lados BA e BC não foram dados e é o que o problema quer, então vamos chamá-los de x e y.

Repare que o enunciado diz que o perímetro (ou seja, a soma de todos os lados) desse triângulo é 50.

Então temos que: x + y + (8 + 12) = 50

                             x + y = 30

                             x = 30 - y     (*)

Note que a bissetriz forma dois pequenos triângulos internos e podemos usar seus lados para montar as proporções.

 x =  y

 8  12

12 x = 8 y ---> Vamos substituir pela informação acima (*)

12. (30 - y) = 8 y

360 - 12 y = 8 y

-20 y  = -360  .(-1)

y = 360 / 20

y = 18

Utilizando novamente (*), temos:

x = 30 - y

x = 30 - 18

x = 12

Refaça o exercício para fixar o que aprendeu. É normal estranhar uma aula a distância, mas não precisa se desesperar. Respire fundo, lembre-se das orientações do primeiro post e refaça o exercício até compreender o passo a passo.

Agora, #bora para a página 18 e 19.

Mais uma vez, repare que as questões 8 e 9 já foram feitas e corrigidas. Hoje faremos as questões 10 até 13.

10- Em determinada hora do dia, a sombra de um prédio, num terreno plano mede 15 m. Nesse mesmo instante, um poste que está próximo ao prédio, e tem 5 m altura projeta uma sombra de 3 m de comprimento. Calcule a altura do prédio.

A imagem dessa questão é mais ou menos assim:

Utilize o que aprendemos sobre semelhança de triângulos e monte a proporção com as informações da imagem. Lembre-se que ele quer a altura do prédio, então chame essa parte de x, ou qualquer outra incógnita.

11- Em um triangulo ABC temos os lados AB = 9 cm, AC = 11 cm e BC = 15 cm. Um triângulo MNP, semelhante ao triangulo ABC, tem 105 cm de perímetro. Determine as medidas dos lados do triângulo MNP.

Vamos lá! Desenhe os dois triângulos. No ABC você coloca os números dados no problema. No MNP, coloque as letras x, y e z, pois não foram dadas essas informações.

Ok! Monte as proporções.

Para resolver essa, é preciso relembrar algumas propriedades da proporção:

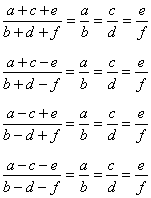
Usando a primeira da lista acima, podemos resolver nosso problema:

Agora, resolva sozinho as questões 12 e 13!

Pronto, Aula I finalizada com sucesso.

Se houver dúvida, poste um comentário que assim que puder estarei respondendo.

Até a próxima.